
Return to the home page for Patrick Kellogg
The “Great Internet Mersenne Prime Search” is a large distributed computing project sponsored by the Mersenne organization at: http://www.mersenne.org/prime.htm. It was started by George Woltman in 1994 to find Mersenne primes, and in the last six years the group has found the four largest ones currently known. In addition to GIMPS, they also sponsor several other distribute mathematical projects at (http://www.mersenne.org/).
Why would anyone want to try to find the next Mersenne prime? Well, besides the altruistic idea of contributing to scientific knowledge, the Electronic Frontier Foundation (www.eff.org) is offering a $100,000 reward to the first person that helps to discover a ten million digit (or higher) prime number. There are some caveats— $25,000 goes to charity and $20,000 to GIMPS, but it still leaves $55,000 for the lucky computer user. And the 1 in 250,000 odds are better than most state lotteries.
Installation of the GIMPS software is easy. Different versions are available for Microsoft Windows 95/98 and NT/2000 (as well as the earlier 3.1), Linux, FreeBSD, OS/2 and DOS. Also, optimized code is available for different platforms, including PowerPC, StrongARM, UNIX, and older x86 machines. Though the software does not support multiple processors or multiple machines working on the same problem, they have a very robust server at “PrimeNet” (http://www.mersenne.org/primenet/) that allows users to start or stop testing, or put the application “on hold” while the user is on vacation or the computer is turned off.
First, I downloaded a Windows 95/98 version to my PC. It was available in both a 675k self-extracting version, as well as a 396k zip file. Version 20 is the latest version, and was released on April 25, 2000. After I installed the software called “Prime95”, it placed an icon in my “system tray” and included itself to run on system startup. I was slightly annoyed that you can't specify the directory name the software is copied into, although you can give it a directory path. Also, it doesn't use the Windows “StartUp” directory (or even SYSTEM.INI) to launch itself on startup, but seems to use an annoying registry setting that causes it to be difficult to uninstall.
Another slightly annoying problem with GIMPS is that they don't seem to be too concerned about security. Passwords are not encrypted by the program, and are shown in plaintext on the user's screen. Also, my user name and computer name are available on the main PrimeNet page for anyone to see. These two names make up my unique GIMPS account, though my email address and IP address were hidden.
The user can also create “teams” of computers they own, or can work jointly with several researchers on a team. Even though the separate computers will not work on the same task, all the processing time will be recorded under the same team. A list of some of the top producing teams is available at: http://www.mersenne.org/top.htm. Not a very dangerous breach of security, but I was still surprised to see user names listed.
Before starting a Mersenne search, the program will test the user's computer to make sure it is running correctly:

This self-test takes about an hour to run. However, once installed, setup is easy. First, the computer asks about the user information and what kind of computer the program will be running on:
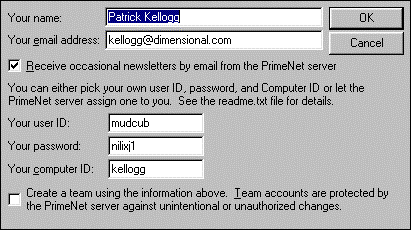
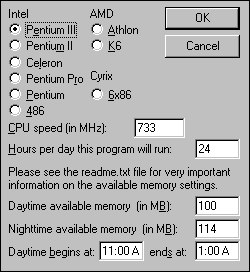
The computer speed (and hours of use) are used to calculate the expected completion date. Periodically, the program can recomputed the expected date, and send the new date to the PrimeNet server. This will often happen while the user is away from the computer. If your computer is not connected to the internet at the time, the program will queue up the message and try later. Unfortunately, it seems to retry at two minute intervals.
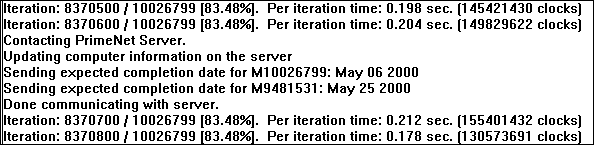
My first Mersenne candidate was started on April 4, 2000. It took until May 7 for the program to verify that it was (sadly) not prime.

The first candidate was 210026799-1. Note that the program also queued up another candidate: 29481531-1. However, the program does not work on the two primes in parallel. Instead, it waited for the first candidate to finish before starting the next one.
As of May 8, my computer showed a new completion date:

The user can specify how much work they would like store in a queue. At least ten days' worth of data seems to be the default. However, the user is not allowed to choose the prime they would like to test.
Here is what my computer reported to PrimeNet about my first prime:
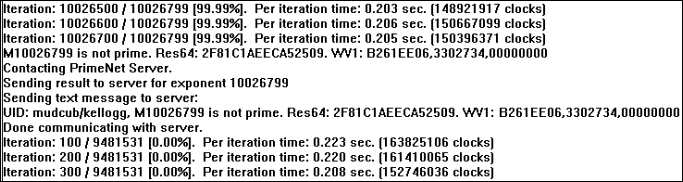
The user can also contact the PrimeNet server for a detailed report of their processing status. There are also detailed reports about the state of the server and what other people are working on. The PrimeNet server wasn't completed until 1997, two years into the GIMPS project, but it is really one of the most impressive parts of the project:
Mersenne PrimeNet Server 4.0 (Build 4.0.031)
Individual Account Report 08 May 2000 00:23 (May 7 2000 5:23PM Pacific)
All dates and times are Coordinated Universal Time (UTC)
EFF.org Research Discovery Prize is US $100,000 for first 10 million-digit prime
Account ID LL P90* Exponents Fact.P90 Exponents P90 CPU
CPU yrs LL Tested CPU yrs* w/ Factor hrs/day
-------------- ------- --------- -------- --------- -------
mudcub 0.491 1 0.000 0 130.35
Contact name :
Contact e-mail : [email protected]
Receive e-mail : YES
Last activity : 08 May 2000 00:09 UTC
Account created: 04 Apr 2000 15:18 UTC
------- Machines Assigned to PrimeNet -------
Intel Pentium III : 1
---------------------- -------
TOTAL, uniquely named : 1
------- Exponents Assigned -------
Assignment overdue check-in is set at 60.0 days (0.0 days to expire)
prime fact current days
exponent bits iteration run / to go / exp date updated date assigned computer ID Mhz Ver
-------- -- ---- --------- ----------------- --------------- --------------- ------------ ---- ---
9481531 64 13.4 17.7 77.7 02-May-00 16:41 24-Apr-00 14:09 kellogg 733 v19
Lucas-Lehmer testing : 1
Factoring only : 0
Double-checking LL : 0
---------------------- -------
TOTAL : 1
------- Exponents Cleared since last Synchronization -------
prime fact Lucas-Lehmer residue or factor
exponent bits [residues partially masked] date returned computer ID
-------- ---- -- -------------------------------- --------------- ------------
10026799 64 0x2F81C1AEECA525__ 08-May-00 00:09 kellogg
Factored composite : 0
Lucas-Lehmer composite: 1
Double-checked LL : 0
---------------------- -------
TOTAL : 1
*P90 CPU time according to Woltman/Kurowski formulation. Calibrated by
benchmark P5 90Mhz, 32.98 MFLOP units: 25658999 FLOP/0.778s (256k FFT).
(c)1997-2000 Entropia.comThe GIMPS factoring code uses a modified “sieve of Eratosthenes”. Each possible factor of a Mersenne prime 2P-1 must be 1 or 7 mod 8. Also, any possible factor must itself be prime. So, we can recursively test for prime factors of the Mersenne candidate.
As studied in theory classes, the probability of finding a factor between 2n and 2 n +1 is about 1/n. So, we can use probability to be reasonably sure that we have searched through enough prime factors to prove that the Mersenne candidate is also prime. The GIMPS software also uses some other techniques to avoid testing too many primes. There is something called Pollard's
(P-1) method, and other probability techniques used to test the primes that are most likely to be factors. I think these two methods allow the program to provide the “chances” that your given candidate is prime (in my case, 1 in 86843).
However, the main mathematic technique GIMPS uses is the Lucas-Lehmer test. It uses the fact that the fastest way to repeatedly square a large number is to use a fast fourier transform. In 1994, Richard Crandall and Barry Fagin showed that an “irrational based” FFT would more than double the repeated squaring by using a smaller FFT. Plus, it check the 2P-1 term at the same time for “free”.
Lucas-Lehmer Test: For p odd, the Mersenne number 2p-1
is prime if and only if 2p-1 divides S(p-1) where S(n+1)
= S(n)2-2, and S(1) = 4. [Proof.]
The pseudocode for this test is:
Lucas_Lehmer_Test(p):
s := 4;
for i from 3 to p do s := s2-2 mod 2p-1;
if s == 0 then
2p-1 is prime
else
2p-1 is composite;
In addition, there are a lot of statistical calculations to discover the calculation error, since we are using floating-point numbers. This is called the “convolution error” and GIMPS handles it by converting the floats into integers and looks at the difference. If it is too high, GIMPS will break the calculation up into different parts and try again.
However, tests for correctness are very expensive, so they are only done intermittently. So, GIMPS also includes a verification step to verify the calculations. There are checksums, residues, and if you are lucky enough to report a Mersenne prime, GIMPS will check your result a little by hand. In fact, you must wait for their verification before you can contact the media and announce you are a $100,000 winner.
More details about the mathematics behind GIMPS is available at: http://www.mersenne.org/math.htm and
http://www.utm.edu/research/primes/mersenne.shtml
Though the GIMPS software is not as “polished” as other distribute computing projects (such as the excellent SETI@Home project, http://setiathome.ssl.berkeley.edu/, with it's incredible 3D screen savers of FFTs in progress), I recommend users to try it out. After all, you might already be a winner!